Answer:
After 7.04 years the amount will reach $57,000 or more
Explanation:
The rule of the compound interest is
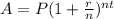 , where
, where
- n is the period of the time
∵ A loan of $36,000 is made at 6.75% interest, compounded annually
∴ P = 36,000
∴ r = 6.75% = 6.75 ÷ 100 = 0.0675
∴ n = 1 ⇒ compounded annually
∵ The amount after t years will reach $57,000 or more
∴ A = 57,000
→ To find t substitute these values in the rule above
∵ 57,000 = 36,000
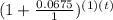
∴ 57,000 = 36,000
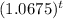
→ Divide both sides by 36,000
∵
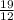 =
=
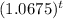
→ Insert ㏒ in both sides
∴ ㏒(
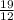 ) = ㏒
) = ㏒
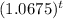
→ Remember ㏒
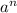 = n ㏒(
= n ㏒(
 )
)
∵ ㏒(
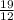 ) = t ㏒(1.0675)
) = t ㏒(1.0675)
→ Divide both sides by ㏒(1.0675)
∴ 7.035151337 = t
∴ t ≅ 7.04
∴ After 7.04 years the amount will reach $57,000 or more