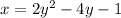Question

1.- What type of parabola is this?

2.- What is the vertex for the parabola?

3.- What is the 'a' value for the given graph?

4.- What is the equation for the given parabola?​

Answer 1

Part 1

Sideways or "horizontal" parabola with a horizontal axis of symmetry.

Part 2

The vertex is the turning point: (-3, 1)

Part 3

Vertex form of a horizontal parabola:

`x=a(y-k)^2+h`

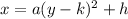
where:

• (h, k) is the vertex
• a is some constant
  If a > 0 the parabola opens to the right.
  If a < 0 the parabola opens to the left.

Point on the curve: (-1, 2)

Substituting the vertex and the found point into the formula and solving for a:

`\implies -1=a(2-1)^2-3`

`\implies -1=a-3`

`\implies a=2`

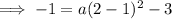
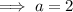
Part 4

Equation for the given parabola in vertex form:

`x=2(y-1)^2-3`

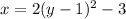
Equation in standard form:

`x=2y^2-4y-1`