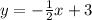Question

A path for a new city park will connect the park entrance to Main Street, as shown to the right. The path should be perpendicular to Main Street. What is an equation that represents the path?

Answer 1

its y=1/2x+4 lol the other guy was 1 off

Explanation:

Answer 2

`y = -(1)/(2)x + 3`

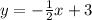
Explanation:

To create an equation in slope-intercept form, y = mx + b, for the path, we need to find slope (m) of the path, and also determine the y-intercept (b) of the path.

First, find the slope of the main street:

Using two points on the main street, (2, 3) and (3, 5),

`slope (m) = (y_2 - y_1)/(x_2 -x_1) = (5 - 3)/(3 - 2) = (2)/(1) = 2`

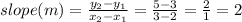
Since the path would be perpendicular to the main street, therefore, the slope of the path would be the negative reciprocal of 2.

Thus, the slope of the path, m = -½.

The y-intercept of the path is the point at which the line of the path cuts across the y-axis.

The path intercepts the y-axis at y = 3. Therefore, the y-intercept (b) = 3.

Substitute m = -½, and b = 3 into
`y = mx + b`.

✅The equation that represents the path would be:

`y = -(1)/(2)x + 3`