Answer:
The average rate of change is
Δy ÷ Δx = -20 ÷ 4
Δy/Δx = -20/4
= -5
Explanation:
Given the function
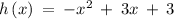
Putting x = 6
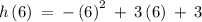
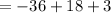
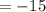
Putting x = 2
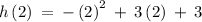
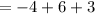
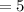
The change in y from 2 to 6 is
Δy = -15 - 5
= -20
The interval from 2 to 6 has a width of
Δx = 6 - 2
= 4
Therefore, the average rate of change is
Δy ÷ Δx = -20 ÷ 4
Δy/Δx = -20/4
= -5