Question

Find the average rate of change of h(x) = - x ^ 2 + 3x + 3 from x = 2 to x = 6 .

Answer 1

The average rate of change is

Δy ÷ Δx = -20 ÷ 4

Δy/Δx = -20/4

= -5

Explanation:

Given the function

`h\left(x\right)\:=\:-x^2\:+\:3x\:+\:3`

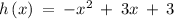
Putting x = 6

`h\left(6\right)\:=\:-\left(6\right)^2\:+\:3\left(6\right)\:+\:3`

`=-36+18+3`

`=-15`

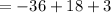
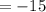
Putting x = 2

`h\left(2\right)\:=\:-\left(2\right)^2\:+\:3\left(2\right)\:+\:3`

`= -4 + 6 +3`

`= 5`

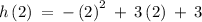
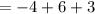
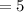
The change in y from 2 to 6 is

Δy = -15 - 5

= -20

The interval from 2 to 6 has a width of

Δx = 6 - 2

= 4

Therefore, the average rate of change is

Δy ÷ Δx = -20 ÷ 4

Δy/Δx = -20/4

= -5