Answer:
the ordered triple of these equations will be:
(x, y, z) = (6, 1, 5)
Explanation:
Given the equations
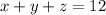
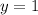
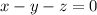
As
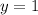
We can get the value of x by adding the first and third equation
so
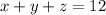
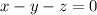
so the equations become
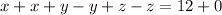
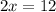
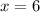
Putting x = 6 and y=1 in the first equation
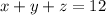
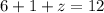
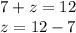
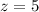
Therefore, the ordered triple of these equations will be:
(x, y, z) = (6, 1, 5)