Question

Please helppp with this math question <333

Answer 1

The average rate of change of the function
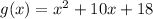`g(x)=x^2+10x+18` over the interval
`-11 \leq x\leq -1` is -1

Explanation:

We are given the function
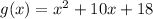`g(x)=x^2+10x+18` over the interval
`-11 \leq x\leq -1`

We need to find average rate of change.

The formula used to find average rate of change is :
`Average \ rate \ of \ change=(g(b)-g(a))/(b-a)`

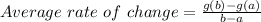
We have b=-1 and a=-11

Finding g(b) = g(-1)

`g(x)=x^2+10x+18\\Putting \ x=-1\\g(-1)=(-1)^2+10(-1)+18\\g(-1)=1-10+18\\g(-1)=9`

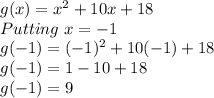
Finding g(a) = g(-11)

`g(x)=x^2+10x+18\\Putting \ x=-11\\g(-11)=(-11)^2+10(-11)+18\\g(-1)=121-110+18\\g(-1)=29`

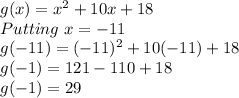
Finding average rate of change

`Average \ rate \ of \ change=(g(b)-g(a))/(b-a)\\Average \ rate \ of \ change=(9-29)/(-1-(-11))\\Average \ rate \ of \ change=(-10)/(-1+11)\\Average \ rate \ of \ change=(-10)/(10)\\Average \ rate \ of \ change=-1`

So, the average rate of change of the function
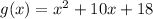`g(x)=x^2+10x+18` over the interval
`-11 \leq x\leq -1` is -1