Answer:
The average rate of change of the function
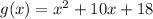 over the interval
over the interval
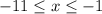 is -1
is -1
Explanation:
We are given the function
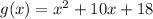 over the interval
over the interval
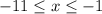
We need to find average rate of change.
The formula used to find average rate of change is :
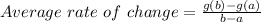
We have b=-1 and a=-11
Finding g(b) = g(-1)
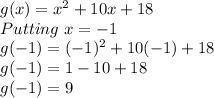
Finding g(a) = g(-11)
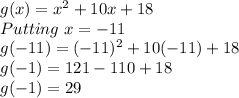
Finding average rate of change
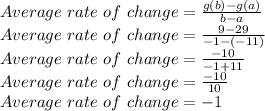
So, the average rate of change of the function
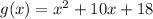 over the interval
over the interval
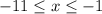 is -1
is -1