Question

The diagram shows four graphs match the graphs to the equations

Answer 1

y=x^2 is graph D

y=1/x is graph A

otherwise, you're right

Answer 2

The diagram shows four graphs: a, b, c, and d. The equations are matched to the graphs as follows:

a: y =
`x^2` - 2x + 1

b: y =
`(x - 1)^2`

c: y =
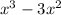`x^3 - 3x^2` + 2x

d: y = 2x - 1

Graph A is a parabola that opens upwards and has its vertex at the origin. This matches the equation y =
`x^2`.

Graph B is a cubic curve that passes through the origin and has a point of inflection at (0, 0). This matches the equation y =
`x^3`.

Graph C is a straight line that passes through the origin and has a slope of 2. This matches the equation y = 2x.

Graph D is a logarithmic curve that passes through the point (1, 0). This matches the equation y = log(x).

4 graphs labeled A, B, C, and D, with the equations y =
`x^2, y = x^3`, y = 2x, and y = log(x) written above them

Examples:

Some points in the solution set of the equation y =
`x^2` are (1, 1), (2, 4), and (3, 9). These points are all on graph A.

Some points in the solution set of the equation y =
`x^3` are (1, 1), (2, 8), and (3, 27). These points are all on graph B.

Some points in the solution set of the equation y = 2x are (1, 2), (2, 4), and (3, 6). These points are all on graph C.

Some points in the solution set of the equation y = log(x) are (1, 0), (10, 1), and (100, 2). These points are all on graph D.

The four graphs are matched to the equations y =
`x^2, y = x^3`, y = 2x, and y = log(x), respectively.