Question

Cliff divers at Acapulco jump into the sea from a cliff 36 meters high. At the level of the sea, there is an outcropping of rock that sticks out a horizontal distance of 6 meters. With what minimum horizontal velocity must the cliff divers leave the top of the cliff if they are to miss this rocky outcropping?

Answer 1

The cliff drivers must leave the top of the cliff at 2.21 m/s

Step-by-step explanation:

Horizontal Motion

When an object is thrown horizontally with a speed v from a height h, it describes a curved path ruled exclusively by gravity until it eventually hits the ground.

The range or maximum horizontal distance traveled by the object can be calculated as follows:

`\displaystyle d=v\cdot\sqrt{\frac {2h}{g}}`

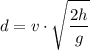
If the range is known and we are required to find the initial speed of launch, then we can solve the above equation for v as follows:

`\displaystyle v=d\cdot\sqrt{\frac {g}{2h}}`

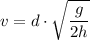
Cliff drivers jump into the sea from a height of h=36 m and must pass over an obstacle d=6 meters away from the cliff.

Let's calculate the speed needed:

`\displaystyle v=6~m\cdot\sqrt{\frac {9.8~m/s^2}{2\cdot 36~m}}`

`\displaystyle v=6~m\cdot\sqrt{\frac {9.8~m/s^2}{72~m}}`

`v=2.21~m/s`

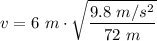
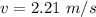
The cliff drivers must leave the top of the cliff at 2.21 m/s