Question

Marcus has been running a beverage cart on weekends at the beach, selling water and soda. Last Saturday, he sold 40 bottles of water and 25 sodas, bringing in $110. Sunday, he sold 50 bottles of water and 45 sodas, making $165. What are the prices for each beverage option?

Answer 1

$2 for soda and $1.5 for a bottle of water

Explanation:

You start by turning both situations into an equation

Let x represent bottles of water and y represent sodas

Saturday:

`40x+25y=110`

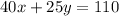
Sunday:

`50x+45y=165`

You then want to start by cancelling out the x in this equation, to do that you want 40x to become -50x so you:

50÷40=1.25

You then times the whole equation by -1.25

40x+25y=110

×-1.25

-50x+-31.25y= -137.5

You then add this equation by Sunday's equation

50x+45y=165

-50x+-31.25y=-137.5

13.75y=27.5

You now want to make the co-efficient of y a whole number (for example 15) so you divide 15/13.75=1.09 recurring

13.75y=27.5

×1.09 recurring

15y=30

15y/15=30/15

y=2

Now that we know y = 2

We can use either Saturday or Sunday's equation to figure out the value of
`x`

Let's use Sunday's:

50x+45×2=165

50x+90=165

50x+90-90=165-90

50x/50=75/50

x=1.5

Let's check our answer with Saturday's equation

40×1.5+25×2=110

This equation is correct

Therefore the prices for each beverage option is $1.5 for a bottle of water and $2 for a soda