Question

A particle travels along a straight line, in a given direction, with constant acceleration. At instant t0 = 0, the magnitude of its velocity is v0 = 5 m/s; at time t = 10s, v = 25m/s. determine:

a) The type of motion of the particle
b) Acceleration
c) The function of velocity in relation to time
d) The velocity at time t = 8.0 s
e) The instant of time in which the velocity module is v = 15m/s

Answer 1

a) The motion described by the particle is undoubtedly a uniformly accelerated rectilinear motion, since the trajectory is rectilinear and the acceleration is constant.

b) In order to calculate the acceleration, we must apply the formula mentioned above, in such a way that the acceleration gives us:

`\boldsymbol{a=(v-v_(o))/(t-t_(o) )=(25-5)/(10-0 )=(20)/(10)=2 \ m/s^2 }`

Our acceleration is 2 meters per second squared.

c) We are asked to calculate the function of velocity in relation to time, we simply substitute in the formula.

`\boldsymbol{v=v0+at }\\\boldsymbol{v=2+5t }`

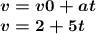
Very easy!!.

d) To know what speed the particle will have at the instant of t = 8s, it is enough to substitute the value of “t” in the previous formula.

`\boldsymbol{v=5+2(8)=5+16=21 \ m/s }`

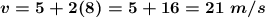
So the speed at time t = 8s is 21 m/s²

e) In this case we are asked to determine at what instant of time the particle will have a speed of 15 m/s, we replace this value in the formula, simply clearing the variable "t", that is:

`\boldsymbol{v=v_(0)+at }`

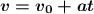
Clearing "t"

`\boldsymbol{t=(v-v_(o))/(a) }`

Substituting the speed value

`\boldsymbol{t=(v-v_(o))/(a)=(15-5)/(2)=(10)/(2)=5 \ seg }`

That is to say that when the particle has a speed of 15 m/s, it will happen exactly at 5 seconds.