Answer:
The second ball has four times as much kinetic energy as the first ball.
Step-by-step explanation:
Kinetic Energy
Is the type of energy an object has due to its state of motion. It's proportional to the square of the speed.
The equation for the kinetic energy is:
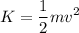
Where:
m = mass of the object
v = speed at which the object moves
The kinetic energy is expressed in Joules (J)
Two tennis balls have the same mass m and are served at speeds v1=30 m/s and v2=60 m/s.
The kinetic energy of the first ball is:
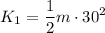

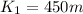
The kinetic energy of the second ball is:

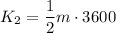

Being m the same for both balls, the second ball has more kinetic energy than the first ball.
To find out how much, we find the ratio:
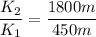
Simplifying:
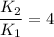
The second ball has four times as much kinetic energy as the first ball.