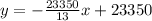Question

1. Delia purchased a new car for $23,350. This make and model straight line depreciates to zero after 13 years.

a. Identify the coordinates of the x- and y- intercepts for the depreciation equation.
b. Determine the slope of the depreciation.
c. Write the straight-line depreciation equation that models this situation.

Answer 1

a. y-intercept = 23350 and x-intercept = 13

b.
`m = -(23350)/(13)`

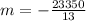
c.
`y = -(23350)/(13)x + 23350`

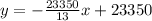
Explanation:

Given

`Years = 13`

`Total\ depreciation = \$23350`

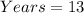
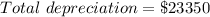
Solving (a): The x and y intercepts

The y intercept is the initial depreciation value

i.e. when x = 0

This value is the value of the car when it was initially purchased.

Hence, the y-intercept = 23350

The x intercept is the year it takes to finish depreciating

i.e. when y = 0

From the question, we understand that it takes 13 years for the car to totally get depreciated.

Hence, the x-intercept = 13

Solving (b): The slope

The slope (m) is the rate of depreciation per year

This is calculated by dividing the total depreciation by the duration.

So:

`m = (23350)/(13)`

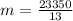
Because it is depreciation, it means the slope represents a deduction.

So,

`m = -(23350)/(13)`

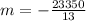
Solving (c): The straight line equation

The general format of an equation is:

`y = mx + b`

Where

`m = slope`

`b = y\ intercept`

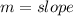
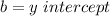
In (a), we have that:

`y\ intercept = 23350`

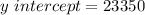
In (b), we have that:

`Slope\ (m) = -(23350)/(13)`

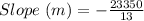
Substitute these values in
`y = mx + b`

`y = -(23350)/(13)x + 23350`

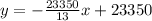
Hence, the depreciation equation is:
`y = -(23350)/(13)x + 23350`