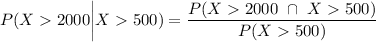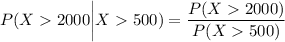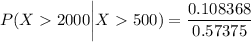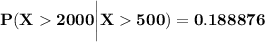Answer:
1. 0.108368
2. 0.188876
Explanation:
Let X be the exponential random variable that represents the lifetime of a computer.
i.e.
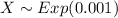
The probability that the computer will function more than 2000 days can be computed as follows:
P(X > 2000)
:
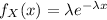
P(X > 2000) = 1 - P(X< 2000)
P(X > 2000) = exp(-2000/β) = e⁻²²
P(X > 2000) = 0.108368
2.
By applying conditional probability;