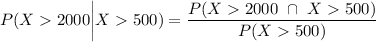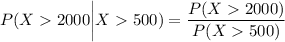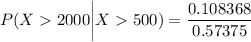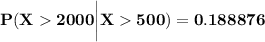Question

The lifetime of a computer can be modeled by an exponential random variable with an expected lifetime of 900 days. 1. Find the probability that the computer will function for more than 2000 days.2. Find the probability that the computer will function for more than 2000 days, given that it’s still working after 500 days.

Answer 1

1. 0.108368

2. 0.188876

Explanation:

Let X be the exponential random variable that represents the lifetime of a computer.

i.e.
`X\sim Exp(0.001)`

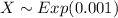
The probability that the computer will function more than 2000 days can be computed as follows:

P(X > 2000)

:
`f_X(x) = \lambda e^{-\lambda x`

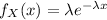
P(X > 2000) = 1 - P(X< 2000)

P(X > 2000) = exp(-2000/β) = e⁻²²

P(X > 2000) = 0.108368

2.

By applying conditional probability;

`P(X>2000 \bigg | X>500) =(P(X>2000 \ \cap \ X>500))/(P(X> 500))`

`P(X>2000 \bigg | X>500) =(P(X>2000 ))/(P(X> 500))`

`P(X>2000 \bigg | X>500) =(0.108368 )/(0.57375)`

`\mathbfP(X>2000 \bigg`