Question

Which function is the inverse of f(x)=-x³-9?​

Answer 1

Answer:B is the answer

Explanation:

Answer 2

Inverse of f(x)=-x^3-9 is
`f^(-1)(x)=\sqrt[3]{-x-9}`

Option B is correct option.

Explanation:

We need to find inverse of
`f(x)=-x^3-9`

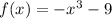
For finding the inverse replace f(x) with y

`y=-x^3-9`

Now, solve for x

Adding 9 on both sides

`y+9=-x^3-9+9\\y+9=-x^3`

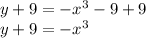
Multiply both sides by -1

`-(y+9)=x^3\\x^3=-y-9`

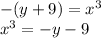
Taking cube root on both sides:

`x^3=-y-9\\\sqrt[3]{x^3} =\sqrt[3]{-y-9} \\x=\sqrt[3]{-y-9}`

Now replace x with f^{-1}(x) and y with x

`f^(-1)(x)=\sqrt[3]{-x-9}`

So, inverse of f(x)=-x^3-9 is
`f^(-1)(x)=\sqrt[3]{-x-9}`

Option B is correct option.