Answer:
attached below is the prove
Explanation:
In order to prove the expression for coefficient b
 we have to find b
we have to find b
 and b
and b

F(x) =
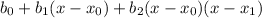
i) Determine b

at x = x

b
 = f(x
= f(x
 )
)
ii) Determine b

at x =

f (
 ) = f (
) = f (
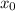 ) + b
) + b

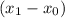 + 0
+ 0
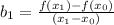
prove of the expression for the coefficient B2 in the quadratic interpolation
attached below is the detailed prove