Question

A certain academic program claims that their students graduate in less than 4 years on average. A random sample of 50 students is taken and the mean and standard deviation are found. The test statistic is calculated to be-169. Using a 5% significance level, the conclusion would be:_________. a) there is sufficient sample evidence for the program's claim to be considered correct b) there is insufficient sample evidence for the program's claim to be considered correct c) there is insufficient sample evidence for the program's claim to be considered incorrect d) there is sufficient sample evidence for the program's claim to be considered incorrect

Answer 1

The correct option is:

(a) There is sufficient sample evidence for the program's claim to be considered correct.

Explanation:

The hypothesis can be defined as follows:

`H_(0):\mu\geq 4\\\\H_(a):\mu< 4`

A random sample of n = 50 students is selected.

The significance level of the test is, α = 0.05.

The degrees of freedom are:

df = n - 1

= 50 - 1

= 49

Compute the critical value as follows:

`t_(\alpha,\ (n-1))=t_(0.05,\ 49)`

`=t_(0.05, 60)\\\\=-1.671`

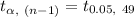
Use the t-table.

Decision rule:

If the calculate value of the test statistic is less than the critical value then the null hypothesis will be rejected.

The calculate value of the test statistic is, t = -1.69.

`cal.t=-1.69<t_(0.05, 49)=-1.671`

The null hypothesis will be rejected at 5% level of significance.

The correct option is:

(a) There is sufficient sample evidence for the program's claim to be considered correct.