If $8,200 is invested in an account earning 5% interest (APR), compounded quarterly. The percentage of growth per year (APY) is 5.09%.
What is the Annual percentage yield?
Using the formula for compound interest:
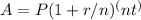
Where:
A = the final amount
P = the principal amount =$8,200
r = the annual interest rate (APR) =5%
n = the number of times interest is compounded per year =4
t = the number of years
Plugging in the values into the formula:
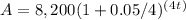
The function showing the value of the account after t years is:

Annual percentage yield (APY):
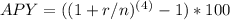
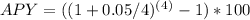
APY= 5.09%
The percentage of growth per year (APY) is 5.09%.