Question

$8,200 is invested in an account earning 5% interest (APR), compounded quarterly.

Write a function showing the value of the account after t years, where the annual
growth rate can be found from a constant in the function. Round all coefficients in
the function to four decimal places. Also, determine the percentage of growth per
year (APY), to the nearest hundredth of a percent.

Answer 1

so comounded monthly
y = 8200(1+(0.046/12))^0.046t

Answer 2

If $8,200 is invested in an account earning 5% interest (APR), compounded quarterly. The percentage of growth per year (APY) is 5.09%.

What is the Annual percentage yield?

Using the formula for compound interest:

`A = P(1 + r/n)^(nt^)`

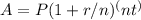
Where:

A = the final amount

P = the principal amount =$8,200

r = the annual interest rate (APR) =5%

n = the number of times interest is compounded per year =4

t = the number of years

Plugging in the values into the formula:

`A = 8,200(1 + 0.05/4)^(^4^t^)`

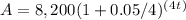
The function showing the value of the account after t years is:

`A(t) = 8,200(1 + 0.0125)^(^4^t^)`

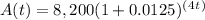
Annual percentage yield (APY):

`APY = ((1 + r/n)^(^4^) - 1) * 100`

`APY = ((1 + 0.05/4)^(^4^) - 1) * 100`

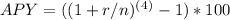
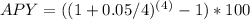
APY= 5.09%

The percentage of growth per year (APY) is 5.09%.