Answer:
The correct option is;
a- 45° only
Explanation:
The given equation can be presented as follows;

We have that cos(2·x) = cos²(x) - sin²(x)
Also, we have, by the difference of two squares, the following relation;
cos²(x) - sin²(x) = (cos(x) - sin(x))(cos(x) + sin(x))
Therefore, the given equation can be written as follows;

Crossing the common term, (cos(x) + sin(x)), in the numerator and the denominator, we have;
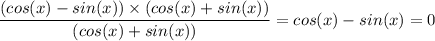
From cos(x) - sin(x) = 0, we have;
Adding sin(x) to both sides of the equation
cos(x) - sin(x) + sin(x) = 0 + sin(x)
cos(x) = sin(x)
Therefore, the opposite leg and the adjacent leg of the right triangle formed with reference to the angle x are equal
∴ x = 90/2 = 45° only for 0° ≤ x ≤ 180°