Answer:
The table shows an exponential function
Explanation:
Linear vs Exponential Functions
A linear function is written as:

where m and b are constants.
If a table contains a linear function, then for each pair of ordered pairs (x1,y1) and (x2,y2), the value of m must be constant.
The slope can be calculated as:
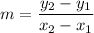
An exponential function is written as:
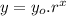
Where r is the ratio and yo is a constant.
If a table contains an exponential function, for two ordered pairs (x1,y1) and (x2,y2), the value of r must be constant.
The ratio can be calculated as:
![\displaystyle r=\sqrt[x2-x1]{(y2)/(y1)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/jo0ky9hbydskra3j19qu4yc6ccssidiuuo.png)
Calculate the slope for (0,4) and (1,2):
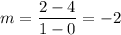
Calculate the slope for (1,2) and (2,1):
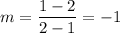
Since the slope is not the same, the function is not linear.
Now calculate the ratio for (0,4) and (1,2)
![\displaystyle r=\sqrt[1-0]{(1)/(2)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/hfl0vvh1hclb91rqaekakqj2hsh0uelqgq.png)
The radical of index 1 is simply equal to its argument:
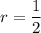
Now calculate the ratio for (0,4) and (2,1)
![\displaystyle r=\sqrt[2-0]{(1)/(4)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/y1b68m809u65f63uj7ob41wxd7l69xs1qa.png)
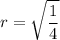
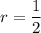
Testing other points we'll find the same ratio, thus the table is an exponential function