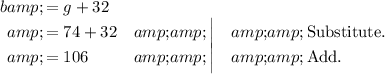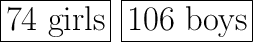
Hey there! This situation can be modeled and solved using a system of equations. We'll use
 to represent the number of boys and
to represent the number of boys and
 to represent the number of girls.
to represent the number of girls.
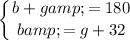
Since we know what
 equals, we can substitute it into the first equation.
equals, we can substitute it into the first equation.

Now that we know the number of girls, use the second equation to get the number of boys.