Question

There were 180 students in attendance at the dance. If there were 32 more boys than girls at the dance, how many girls and boys were at the dance?

Answer 1

`\huge\boxed{\text{$74$ girls}}\ \huge\boxed{\text{$106$ boys}}`

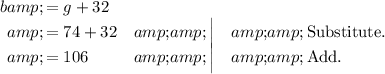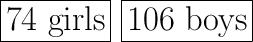
Hey there! This situation can be modeled and solved using a system of equations. We'll use
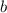`b` to represent the number of boys and
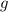`g` to represent the number of girls.

`\displaystyle{\left \{ {{b+g&=180} \atop {b&=g+32} \right.}`

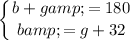
Since we know what
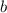`b` equals, we can substitute it into the first equation.

`\begin{aligned}b+g&=180\\(g+32)+g&=180&&\smash\Big&&\text{Substitute.}\\2g+32&=180&&\smash\Big&&\text{Combine like terms.}\\2g&=148&&\smash\Big&&\text{Subtract $32$ from both sides.}\\g&=74&&\smash\Big&&\text{Divide both sides by $2$.}\end{aligned}`

Now that we know the number of girls, use the second equation to get the number of boys.

`\begin{aligned}b&=g+32\\&=74+32&&\smash\Big&&\text{Substitute.}\\&=106&&\smash\Big&&\text{Add.}\end{aligned}`