Question

0:
Question 3
find y intercept of the line using (2,1), (3,-10)

Answer 1

`\huge\boxed{(0, 23)}`

Hey there! We'll solve this problem in three main steps. First, we'll find the slope of the line. Then, we'll find the equation line in point-slope form. Finally, we'll change the equation to slope-intercept form so we can tell what the y-intercept is.

We can use the slope formula, where
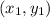`(x_1, y_1)` and
`(x_2, y_2)` are two known points on the line.

`\begin{aligned}m&=(y_2-y_1)/(x_2-x_1)&&\smash\Big&&\text{Use the slope formula.}\\&=(-10-1)/(3-2)&&\smash\Big&&\text{Substitute in the known values.}\\&=(-11)/(1)&&\smash\Big&&\text{Subtract.}\\&=\boxed{-11}&&\smash\Big&&(x)/(1)=x\end{aligned}`

Now that we have the slope, we can use it together with one of the points to get the line in point-slope form. Then, we can distribute and add to get the line in slope-intercept form.

`\begin{aligned}y-y_1&=m(x-x_1)&&\smash\Big&&\text{Use point-slope form.}\\y-1&=-11(x-2)&&\smash\Big&&\text{Substitute in the slope and one point.}\\y-1&=-11x+22&&\smash\Big&&\text{Distribute.}\\y&=-11x+\boxed{23}&&\smash\Big&&\text{Add $1$ to both sides.}\end{aligned}`

We can now clearly see that the y-intercept of the line is
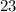`23`, or
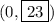`(0, \boxed{23})` as a point.