Question

Anna is sitting in a moving cart and throws a ball straight up. Theoretically, the ball should land in the cart, but it lands on the ground a little before the cart. What is the reason for the difference in the ranges of the ball and the cart?

Answer 1

The difference in the ranges of the ball and the cart is due to projectile motion. The ball follows a parabolic trajectory while the cart continues to move forward.

Step-by-step explanation:

The reason for the difference in the ranges of the ball and the cart is due to the concept of projectile motion. When Anna throws the ball straight up, it follows a curved path known as a parabolic trajectory. The ball goes up and then comes back down due to the force of gravity.

However, while the ball is in the air, the cart continues to move forward. This means that by the time the ball comes back down, the cart has moved a certain distance forward. As a result, the ball lands on the ground slightly before the cart.

Answer 2

Reason for the difference in the ranges of the ball and the cart:

"the average speed of the cart is less than the instant speed of the cart at the time of throwing the ball".

Step-by-step explanation:

Assuming that the air friction is negligible.

Given that the ball lands on the ground a little before the cart.

So, the range of the ball is more than the range of the cart in the same time interval.

Let the instant speed of the cart is v m/s at the time of throwing the ball in the vertically upward direction, so the speed of the ball in the horizontal direction = v m/s.

Let t be the total time of flight of the ball.

As the gravitational force is acting in the downward direction so it will not change the horizontal velocity of the ball.

So, the range covered by the ball
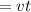`= vt` m.

Let u be the average speed of the cart for the time t s (same as the time of flight of ball).

So, the distance by the cart
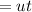`= ut` m

As the range of the ball is more than the range of the cart in the same time interval, so

`vt > ut \\\\\Rightarrow v>u.`

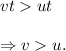
So, the reason for the difference in the ranges of the ball and the cart is "the average speed of the cart is less than the instant speed of the cart at the time of throwing the ball".