Question

LCM of a2+b2 and a4-b4​

Answer 1

The LCM is:

`(a^2+b^2)(a+b)(a-b)`

Explanation:

Given polynomials are:

`a^2+b^2\\a^4 - b^4`

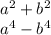
We can use factorization to find the LCM of the given polynomials.

Taking the second polynomial, using the identity

`a^2 - b^2 = (a+b)(a-b)`

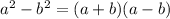
Applying on 2nd polynomial

`(a^2)^2-(b^2)^2\\=(a^2+b^2)(a^2-b^2)\\=(a^2+b^2)(a+b)(a-b)`

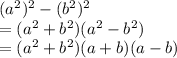
We can see that
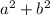`a^2+b^2` is common in both polynomials, it will be counted only one time. The LCM of given polynomials is:

`(a^2+b^2)(a+b)(a-b)`