Question

The lines represented by the equations 20y−24x=−20 and 5y−6x=−5 are...

a)perpendicular
b)the same line
c)neither parallel nor perpendicular
d)parallel

Answer 1

Choice B

Explanation:

The best way to compare two lines is to solve for y.

The first equation:

For
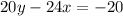`20y-24x=-20` the first thing we should do is add the 24x on both sides which will cancel out itself on the left side
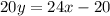`20y=24x-20`. Now all we have to do is divide the 20 on both sides to leave us with
`y=(6)/(5)-1`.

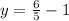The second equation:

For
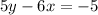`5y-6x=-5` the first thing we should do is add the 6x on both side which will cancel itself on the left side
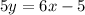`5y=6x-5`. Now all we have to do is divide the 5 on both sides to leave us with
`y=(6)/(5)x-1`.

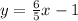Now for the comparison:

They are the same exact line. If you were to graph them they would overlap each other.

Answer 2

parallel i think

Explanation:

parallel because it's a unknown error