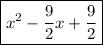We can factorize the quadratic as
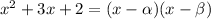
and expanding the right side leads to
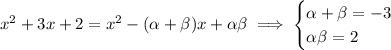
The polynomial we want will have the factorization and expanded form
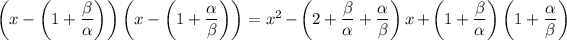
and notice that the constant term is actually the same as (but has the opposite sign of) the coefficient of the
 term :
term :
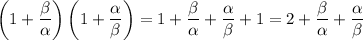
Rewrite the coefficient as
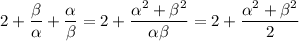
Now, observe that

Then the coefficient is simply
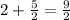 , so the polynomial we want is
, so the polynomial we want is