Answer/Step-by-step explanation:
a. The mistake was "Going to Step 1".
The specific part of the problem that is wrong is

b. It is wrong because applying the negative exponent rule (i.e.
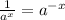 , we should have:
, we should have:
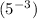 NOT
NOT
 , because
, because
 .
.
c. Here's how to work out the rest of the problem correctly.
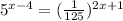
1.
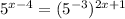
2.
 (distributive property)
(distributive property)
3.
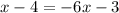 (5 cancels 5)
(5 cancels 5)
4.
 (addition property of equality)
(addition property of equality)
5.
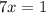 (addition property of equality)
(addition property of equality)
6.
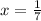 (division property of equality)
(division property of equality)