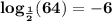Answer:
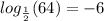
Explanation:
Properties of Logarithms
We'll recall below the basic properties of logarithms:
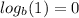
Logarithm of the base:
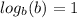
Product rule:

Division rule:
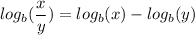
Power rule:
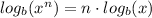
Change of base:
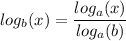
Simplifying logarithms often requires the application of one or more of the above properties.
Simplify

Factoring
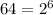 .
.

Applying the power rule:
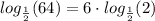
Since
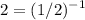
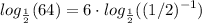
Applying the power rule:
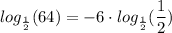
Applying the logarithm of the base: