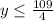Question

The football coach threw a football from a platform to his

quarterback below. The height of the football, h, at time t seconds is modeled by the equation h(t) = -16t^2 + 28t + 15.
1. What is the maximum height of the ball?
2. If the quarterback caught the ball at a height of 6 feet, how many seconds was the ball in the air?
3. Give the domain and range of the function.

Answer 1

1)27.25 feet

2)-0.2774,2.027

3)Domain = All real numbers

Range = y∈R :
`y \leq (109)/(4)`

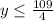
Explanation:

The height of the football, h, at time t seconds is modeled by the equation
`h(t) = -16t^2 + 28t + 15`

General quadratic equation :
`ax^2=bx+c=0`

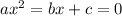
1) Maximum height will be at
`(-b)/(2a)=(-28)/(2(-16))=(7)/(8)`

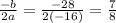
To find maximum height Substitute
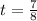`t = (7)/(8)` in the given equation

`h(t)=-16((7)/(8))^2+28((7)/(8))+15\\h(t)=27.25 feet`

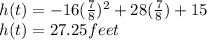
2)

Substitute h(t)=6

So,
`-16t^2+28t+15=6`

`-16t^2+28t+9=0\\t=(-b\pm√(b^2-4ac))/(2a)\\t=(-28\pm √(28^2-4(-16)(9)))/(2(-16))\\t=(-28+ √(28^2-4(-16)(9)))/(2(-16)),(-28- √(28^2-4(-16)(9)))/(2(-16))\\t=-0.2774,2.027`

3)

Domain = All real numbers

Range = y∈R :
`y \leq (109)/(4)`