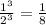Answer:
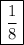
Keys:
•
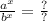
For this problem, the exponents will be 3 since the coin is being tossed 3 times, meaning we multiply the number next to the exponent by itself the number of times the exponent says to. On the other hand, we have two sides of a coin; heads and tails, so we represent heads with the fraction of one-half.
Explanation: