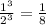Question

What is the probability of tossing a penny and landing on heads three times in a row

Answer 1

`\boxed {(1)/(8)}`

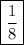
Keys:

•
`(a^x)/(b^x) = (?)/(?)`

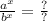
For this problem, the exponents will be 3 since the coin is being tossed 3 times, meaning we multiply the number next to the exponent by itself the number of times the exponent says to. On the other hand, we have two sides of a coin; heads and tails, so we represent heads with the fraction of one-half.

Explanation:

`(1^3)/(2^3) = (1)/(8)`

Answer 2

`|\Omega|=2^3=8\\|A|=1\\\\P(A)=(1)/(8)=12.5\%`