Answer:
Exponential Function
General form of an exponential function with base
 :
:

where:
- A is the y-intercept
- e (Euler's number) is the base
- k is some constant
Question 30
The curve crosses the y-axis at y = 40. Therefore, A = 40.
Substitute the found value of A into the formula along with (1, 56) and solve for
 :
:
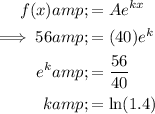
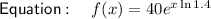
To find the population in 10 years, substitute
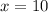 into the found equation:
into the found equation:
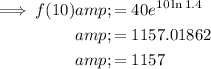
Question 31
The curve crosses the y-axis at y = 10. Therefore, A = 10.
Substitute the found value of A into the formula along with (1, 18) and solve for
 :
:
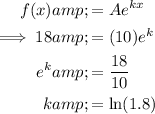
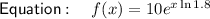
To find the population in 8 years, substitute
 into the found equation:
into the found equation:
