Answer:
(a) The maximum height of the ball is 16 feet at 1 seconds.
(b) The ball hits the ground at 2 seconds.
PART (A) :
Given function: h(t) = -16t² + 32t
Comparing to quadratic function: ax² + bx + c
In this function: a = -16, b = 32, c = 0
To find the maximum height, use the vertex formula:
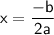
Insert values

Then find h(t) = -16(1)² + 32(1) = 16 feet
Conclusion: The maximum height of the ball is 16 feet at 1 seconds.
PART (B) :
When the ball hits the ground, the height [h(t)] will be 0 ft
-16t² + 32t = 0
-16t(t - 2) = 0
-16t = 0, t - 2 = 0
t = 0, t = 2
The ball hits the ground at 2 seconds. Note: the other 0 seconds is for when the ball was launched at the beginning.