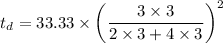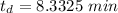Solution :
Given :
Height at which the metal is poured, h = 10 in
Diameter of the runner , d = 0.4 in
Assume viscosity, μ = 0.004 Pa-s
Now considering Bernoulli's equation to find velocity,
As there is no loss in energy, Δ Pressure energy ≅ 0
So,

Here 1 and 2 represents top and bottom section of the sprue.
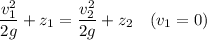
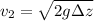
Now substituting
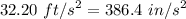 for g and 10 in for Δz in velocity equation,
for g and 10 in for Δz in velocity equation,
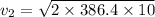
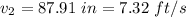
Calculating the area of the basin
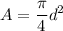
Substitute .04 in for d in the above equation
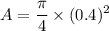
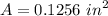
Calculating the flow rate
Q = 0.1256 x 87.91
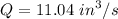
Hence the viscosity is
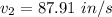 and the flow rate is
and the flow rate is

Calculating the Reynolds number of the flow,
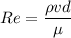
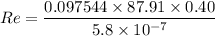
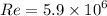
Therefore, the flow is turbulent.
Now considering the solidification time,
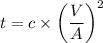
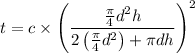

Substituting 1.5 for d and 3 for h and 3 min for t to calculate the value of c is
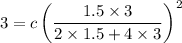
c = 33.33
For case when height is double i.e. h = 6 in
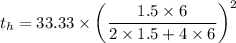
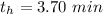
For case when the diameter is doubled i.e. 3 in for d and 3 in for h,