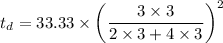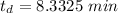Question

Pure aluminum is poured into a sand mold. The metal level in the pouring basin is 10 in. above the metal level in the mold, and the runner is circular with a 0.4-in. diameter. What are the velocity and rate of the flow of the metal into the mold? Is the flow turbulent or laminar? 10.44 A cylinder with a diameter of 1.5 in. and height of 3 in. solidifies in 3 minutes in a sand casting operation. What is the solidification time if the cylinder height is doubled? What is the time if the diameter is doubled?

Answer 1

Given :

Height at which the metal is poured, h = 10 in

Diameter of the runner , d = 0.4 in

Assume viscosity, μ = 0.004 Pa-s

Now considering Bernoulli's equation to find velocity,

As there is no loss in energy, Δ Pressure energy ≅ 0

So,

`$(v^2_1)/(2g)+z_1=(v^2_2)/(2g)+z_2$`

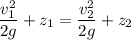
Here 1 and 2 represents top and bottom section of the sprue.

`$(v^2_1)/(2g)+z_1=(v^2_2)/(2g)+z_2 \ \ \ (v_1=0)$`

`$v_2=√(2g \Delta z)$`

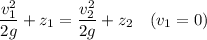
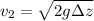
Now substituting
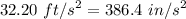`$32.20 \ ft/s^2 = 386.4 \ in/s^2$` for g and 10 in for Δz in velocity equation,

`$v_2=√(2 * 386.4 * 10)$`

`$v_2= 87.91 \ in\s = 7.32 \ ft/s$`

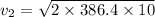
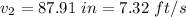
Calculating the area of the basin

`$A=(\pi)/(4)d^2$`

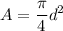
Substitute .04 in for d in the above equation

`$A =(\pi)/(4) * (0.4)^2$`

`$A= 0.1256 \ in^2$`

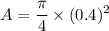
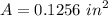
Calculating the flow rate

Q = 0.1256 x 87.91

`$ Q= 11 .04 \ in^3/s $`

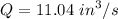
Hence the viscosity is
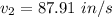`$v_2 = 87.91 \ in/s$` and the flow rate is
`$Q=11.04 \ in^3/s$`

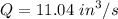
Calculating the Reynolds number of the flow,

`$Re = (\rho v d)/(\mu)$`

`$Re = (0.097544 * 87.91 * 0.40)/(5.8 * 10^(-7))$`

`$Re=5.9 * 10^6$`

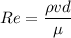
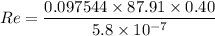
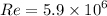
Therefore, the flow is turbulent.

Now considering the solidification time,

`$t=c * \left((V)/(A)\right)^2$`

`$t=c * \left(((\pi)/(4)d^2h)/(2\left((\pi)/(4)d^2\right)+ \pi dh)\right)^2$`

`$t=c\left((dh)/(2d+4h)\right)^2$`

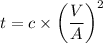
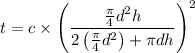
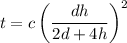
Substituting 1.5 for d and 3 for h and 3 min for t to calculate the value of c is

`$3=c\left((1.5 * 3)/(2 * 1.5 + 4 * 3) \right)^2$`

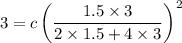
c = 33.33

For case when height is double i.e. h = 6 in

`$t_h = 33.33 * \left((1.5 * 6)/(2 * 1.5 + 4 * 6) \right)^2$`

`$t_h= 3.70 \ min$`

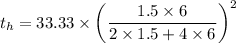
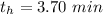
For case when the diameter is doubled i.e. 3 in for d and 3 in for h,

`$t_d = 33.33 * \left((3 * 3)/(2 * 3 + 4 * 3) \right)^2$`

`$t_d= 8.3325 \ min$`