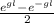Answer:
A) 282.34 - j 12.08 Ω
B) 0.0266 + j 0.621 / unit
C)
A = 0.812 < 1.09° per unit
B = 164.6 < 85.42°Ω
C = 2.061 * 10^-3 < 90.32° s
D = 0.812 < 1.09° per unit
Step-by-step explanation:
Given data :
Z ( impedance ) = 0.03 i + j 0.35 Ω/km
positive sequence shunt admittance ( Y ) = j4.4*10^-6 S/km
A) calculate Zc
Zc =
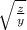 =
=
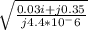
=
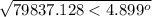 = 282.6 < -2.45°
= 282.6 < -2.45°
hence Zc = 282.34 - j 12.08 Ω
B) Calculate gl
gl =
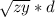
d = 500
z = 0.03 i + j 0.35
y = j4.4*10^-6 S/km
gl =
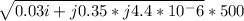
=
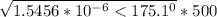
= 0.622 < 87.55 °
gl = 0.0266 + j 0.621 / unit
C) exact ABCD parameters for this line
A = cos h (gl) . per unit = 0.812 < 1.09° per unit ( as calculated )
B = Zc sin h (gl) Ω = 164.6 < 85.42°Ω ( as calculated )
C = 1/Zc sin h (gl) s = 2.061 * 10^-3 < 90.32° s ( as calculated )
D = cos h (gl) . per unit = 0.812 < 1.09° per unit ( as calculated )
where : cos h (gl) =
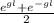
sin h (gl) =