Answer:
Step-by-step explanation:
RC low Pass Filter is an electronic circuit that comprises of a resistor and capacitor and it functions to permit low-frequency signals depending on the design and reject the high-frequency signals above a given frequency known as the cutoff frequency.
From the diagram attached below:
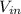 = the input signal
= the input signal
 = the output signal
= the output signal
Since;
 is used across the capacitor C,
is used across the capacitor C,
By using the potential divider equation we have:
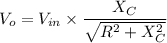
From above;
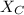 = capacitive reactance ;
= capacitive reactance ;
and The total impedance Z is illustrated as
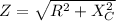
Thus;
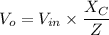
Recall that;
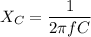
Here; f denotes the frequency of the input signal
Since the cutoff frequency is related to the frequency at which the capacitive reactance and resistance are said to be the same, then:
The Cutoff frequency can be expressed as:
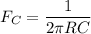
Also;
the frequency of input signal

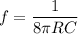
Hence;
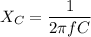
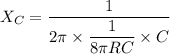
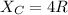
Finally;
From
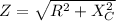
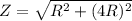
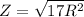
Z
 4.12R
4.12R
As such, the output will be:
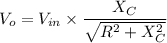
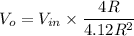
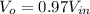
So, if we regard
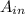 to be the input amplitude, then
to be the input amplitude, then
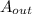 i.e the output amplitude will also be
i.e the output amplitude will also be
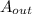 =
=
