Question

In a survey of 468 registered voters, 152 of them wished to see Mayor Waffleskate lose her next election. The Waffleskate campaign claims that no more than 32% of registered voters wish to see her defeated. Does the 95% confidence interval for the proportion support this claim?

a. The reasonableness of the claim cannot be determined.
b. Yes
c. No

Answer 1

Answer: b. Yes

Explanation: Confidence Interval for a population proportion is calculated as:

p ±
`z\sqrt{(p(1-p))/(n) }`

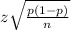
where

p is the sample proportion

n is sample size

z is z-score, in this case, as it is 95%, z-score=1.96

Calculating confidence interval:

`p=(152)/(468)`

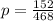
p = 0.3248

0.3248 ±
`1.96\sqrt{(0.3248(0.6752))/(468) }`

0.3248 ±
`1.96√(0.000468)`

0.3248 ± 0.0425

Interval: 0.2823 < μ < 0.3673

The interval means we are 95% sure the true mean is between 0.2823 and 0.3673. As the campaign claims a proportion of no more than 0.32 of the voters wants to see Mayor Waffleskate defeated and the number is in the confidence interval, the claim is supported.