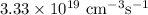Answer:
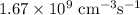
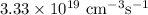
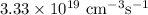
Step-by-step explanation:
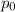 = Hole concentration =
= Hole concentration =
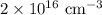
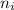 = Intrinsic concentration =
= Intrinsic concentration =
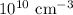
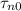 = Minority carrier life time =
= Minority carrier life time =
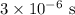
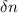 = Excess concentration of electrons =
= Excess concentration of electrons =
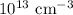
Majority carrier electron concentration is given by
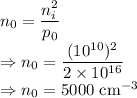
Recombination rate is given by
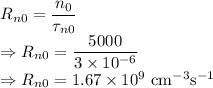
The recombination rate is
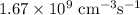
Recombination rate is given by
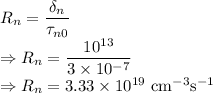
The recombination rate is
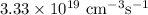
Change in the recombination rate is
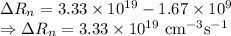
The change in the recombination rate is