NO LINKS!!! This is NOT MULTIPLE CHOICE!!! 13. y = (x + 1)^2 - 2 a. What type of function? b. How do you translate the parent function to produce the equation?

Question

asked Jun 4, 2023 30.6k views

2 Answers

Rld · Answer 1 · 2023-06-06T14:29:25+0000

13.
y=(x-1)^(2) -2

a. Quadratic Function

b. The parent function is
y=x^(2) . Shift
units to the left, shift
units downward.

-Hope this helped :)

Tomas Chabada · Answer 2 · 2023-06-09T01:37:02+0000

Answer:

Given equation:
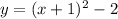
y=(x+1)^2-2

The function is a quadratic function in vertex form:
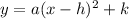
y=a(x-h)^2+k

Translations

For
a > 0

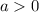
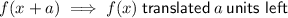
$f(x+a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units left}$

$f(x-a) \implies f(x) \: \textsf{translated}\:a\:\textsf{units right}$

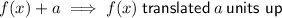
$f(x)+a \implies f(x) \: \textsf{translated}\:a\:\textsf{units up}$

$f(x)-a \implies f(x) \: \textsf{translated}\:a\:\textsf{units down}$

Parent function:
f(x)=x^2

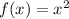
Translations

Translated 1 unit left:
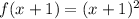
f(x+1)=(x+1)^2

Then translated 2 units down:
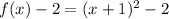
f(x)-2=(x+1)^2-2

Therefore, translate the parent function by 1 unit left and 2 units down to produce the given equation.