Answer:
The ball will go as high as 8.46 m
Step-by-step explanation:
Projectile Motion
It's the type of motion that experiences an object launched at a certain height above the ground and moves along a curved path exclusively under the action of gravity.
Being vo the initial speed of the object, θ the initial launch angle, and g the acceleration of gravity, then the maximum height hm can be calculated as follows:
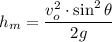
The soccer ball is kicked at a speed of vo=24 m/s at an angle of θ=31°. Taking the value of
 , then:
, then:
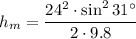
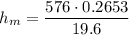

The ball will go as high as 8.46 m