Question

Consider w=sqrrt2/2(cos(225°) + isin(225°)) and z = 1(cos(60°) + isin(60°)). What is w+ z expressed in rectangular form?

Answer 1

Option (3)

Explanation:

w =
`(√(2))/(2)[\text{cos}(225) + i\text{sin}(225)]`

Since, cos(225) = cos(180 + 45)

= -cos(45) [Since, cos(180 + θ) = -cosθ]

= -
`(√(2))/(2)`

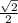
sin(225) = sin(180 + 45)

= -sin(45)

= -
`(√(2))/(2)`

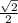
Therefore, w =
`(√(2))/(2)[-(√(2))/(2)+i(-(√(2))/(2))]`

=
`-(2)/(4)(1+i)`

=
`-(1)/(2)(1+i)`

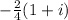
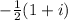
z = 1[cos(60) + i(sin(60)]

=
`[(1)/(2)+i((√(3))/(2))`

=
`(1)/(2)(1+i√(3))`

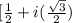
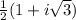
Now (w + z) =
`-(1)/(2)(1+i)+(1)/(2)(1+i√(3))`

=
`-(1)/(2)-(i)/(2)+(1)/(2)+i(√(3))/(2)`

=
`((i√(3)-i))/(2)`

=
`((√(3)-1)i)/(2)`

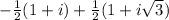
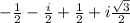
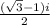
Therefore, Option (3) will be the correct option.