Answer:
Option (3)
Explanation:
w =
![(√(2))/(2)[\text{cos}(225) + i\text{sin}(225)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/a1xbwzf1zls3cy1ke1oqjc0u3z6f4i6d4h.png)
Since, cos(225) = cos(180 + 45)
= -cos(45) [Since, cos(180 + θ) = -cosθ]
= -
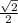
sin(225) = sin(180 + 45)
= -sin(45)
= -
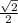
Therefore, w =
![(√(2))/(2)[-(√(2))/(2)+i(-(√(2))/(2))]](https://img.qammunity.org/2021/formulas/mathematics/high-school/318bxqxvbqs5ztinu7ghsux0yc9du53jz9.png)
=
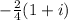
=
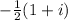
z = 1[cos(60) + i(sin(60)]
=
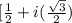
=
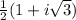
Now (w + z) =
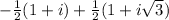
=
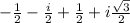
=
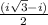
=
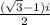
Therefore, Option (3) will be the correct option.