Answer:
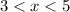
Explanation:
Given inequality:

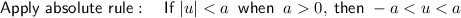


Therefore:
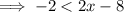
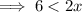
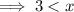
And:
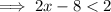

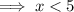
Merge the overlapping intervals:
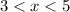
Proof
Graph:
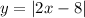
Add a line at
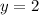
The interval that satisfies
 is the area under the points of intersection (shaded area on the attached graph).
is the area under the points of intersection (shaded area on the attached graph).
The values of x when
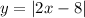 is less than 2 is more than x = 3 and less than x = 5.
is less than 2 is more than x = 3 and less than x = 5.