Answer:
12 hours
Explanation:
Let w = Wilma alone
Let k = Kyle alone
Let t = Working together
Given the following data;
Time it took Wilma = 4 hours
Time it took them together = 3 hours
Time it took Kyle = x
To find the time it will take Kyle, we would use this arithmetical expression;
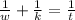
Substituting into the equation, we have;
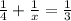
Lowest common denominator (LCD) = 12x
Multiplying all through by "12x" we have;
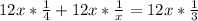
Simplifying the equation, we have;
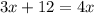
Rearranging the equation, we have;
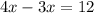
x = 12 hours.
Therefore, it would take Kyle 12 hours to mow if he worked alone.