Question

Solve Problem 1 on a cold air-standard basis with specific heats evaluated at

300 K.

1. An air-standard Otto cycle has a compression ratio of 9. At the beginning of
compression, 1 = 100 kPa and 1 = 300 K. The heat addition per unit mass
of air is 1350 kJ/kg. Determine
(a) the net work, in kJ per kg of air.
(b) the thermal efficiency of the cycle.
(c) The mean effective pressure, in kPa.
(d) The maximum temperature in the cycle, in K.

Answer 1

(a) 774.529 kJ/kg

(b) Approximately 61.2%

(c) 96.816 kPa

(d) The maximum in the cycle temperature is 2655.3 K

Step-by-step explanation:

(a)The temperature T₂ = T₁ × r^(k - 1)

∴ T₂ = 300 × 9^(1.4 - 1) = 772.467 K

P₂ = P₁×r×T₂/T₁ = 100 × 8 × 772.467/300 = 2059.912 kPa

W₁₂ = Cv × (T₁ - T₂) = 0.717*(300 - 772.467) ≈ -338.76 kJ/kg

The heat added = q₂₃ = 1350 kJ/kg = Cv × (T₃ - T₂) = 0.717*(T₃- 772.467)

1350/0.717 = T₃- 772.467

T₃ = 1350/0.717 + 772.467 = 2655.3 K

T₄ = T₃ × (1/r)^(k - 1) = 2655.3 × (1/9)^(1.4 - 1) = 1102.596 K

W₃₄ = Cv×(T₃ - T₄) = 0.717 × (2655.3 - 1102.596) ≈ 1113.289 kJ/kg

The net work = W₁₂ + W₃₄ = -338.76 + 1113.289 = 774.529 kJ/kg

(b) The thermal efficiency,
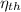`\eta _(th)` = 1 - T₁/T₂ = (1 - 300/772.467) × 100 ≈ 61.2%

(c) The Mean Effective Pressure, MEP = (Net work)/Displacement Volume)

For unity clearance, volume, we have;

MEP = 774.529/(9 - 1) = 96.816 kPa

(d) The maximum temperature, occur at T₃ = 2655.3 K.